भारतीय ज्योतिष और पञ्चाङ्ग
अरुण कुमार उपाध्याय, भुवनेश्वर
मो-०९४३७०३४१७२
ज्योतिष
ज्योतिष => ज्योति => प्रकाश
आकाश में २ प्रकार की ज्योति हैं।
०१. स्वयं प्रकाशित: जैसे सूर्य, या अन्य तारा।
०२. दूसरे से प्रकाशित: जैसे चन्द्र सूर्य प्रकाश से प्रकाशित है। पृथ्वी तथा अन्य ग्रह मंगल, बृहस्पति आदि सूर्य से प्रकाशित हैं। आकाश में तारा समूह, सूर्य के ग्रहों की स्थिति और गति का अध्ययन ज्योतिष है।
कैलेण्डर
काल गणना: किसी समय से अब तक कितना समय बीता उसको वर्ष, मास, दिन में गिनते हैं। इसे कैलेण्डर कहते हैं। संस्कृत में कलन = संख्या या गणना।
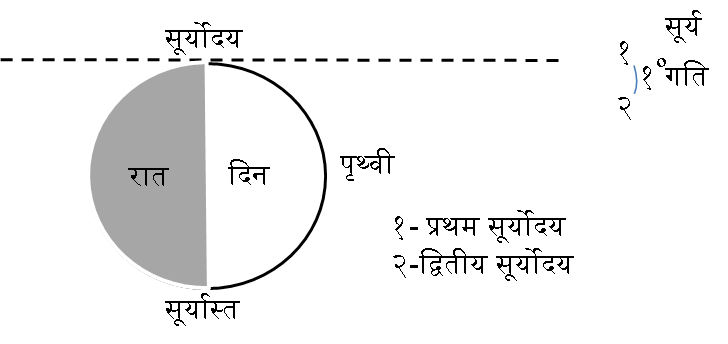
दिन: सूर्योदय से अगले सूर्योदय तक का समय
मास: चन्द्र की पूर्णिमा से पूर्णिमा का समय
वर्ष: ऋतु आरम्भ से अगले ऋतु आरम्भ तक, सूर्य के चारो तरफ पृथ्वी की परिक्रमा।
रोमन कैलेण्डर में दिन की संख्या मास के आरम्भ से १, २, ३…३० या ३१ तक करते हैं (तिथि)।
इसके साथ ७ ग्रहों के नाम पर ७ वार हैं— रवि (सूर्य), सोम (चन्द्र), मंगल, बुध, गुरु, शुक्र, शनि
पञ्चाङ्ग
भारत में ५ प्रकार से दिन लिखते हैं। अतः यहां की काल गणना को पञ्चाङ्ग (५ अङ्ग) कहते हैं।
५ अङ्ग हैं—
०१. तिथि: चन्द्र का प्रकाश १५ दिन तक बढ़ता है। यह शुक्ल पक्ष है जिसमें १ से १५ तक तिथि है। कृष्ण पक्ष में १५ दिनों तक चन्द्र का प्रकाश घतता है। इसमें भी १ से १५ तिथि हैं।
०२. वार: ७ ग्रहों के नाम पर ७ वार— रवि (सूर्य), सोम (चन्द्र), मंगल, बुध, गुरु, शुक्र, शनि।
०३. नक्षत्र: चन्द्र २७.३ दिन में पृथ्वी का चक्कर लगाता है। १ दिन में आकाश के जितने भाग में चन्द्र रहता है, वह उसका नक्षत्र है। ३६० अंश के वृत्त को २७ भाग में बांटने पर १ नक्षत्र १३ १/३ अंश का है। चन्द्र जिस नक्षत्र में रहता है, वह उस दिन का नक्षत्र हुआ।
०४. योग: चन्द्र तथा सूर्य की गति का योग कर नक्षत्र के बराबर दूरी तय करने का समय योग है। २७ योग २५ दिन में पूरा होते हैं।
०५. करण: तिथि के आधे भाग को करण कहते हैं।
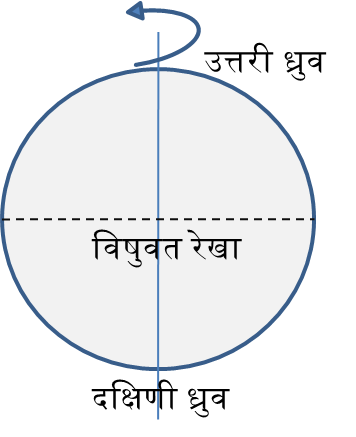
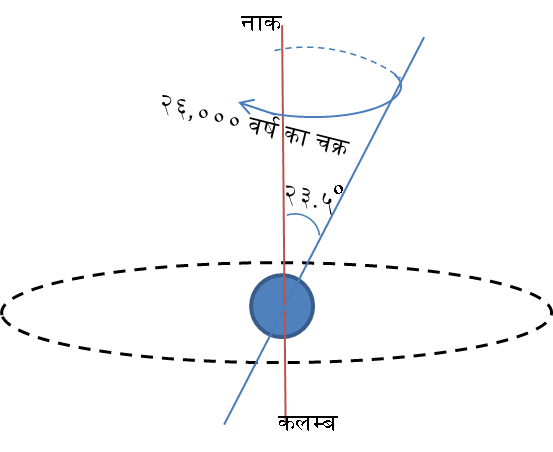
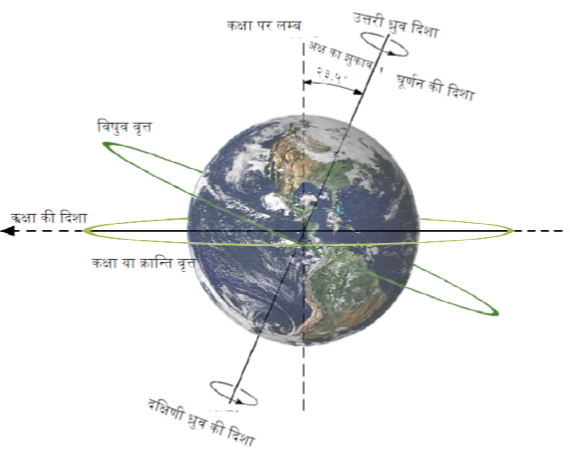
पृथ्वी की दैनिक गति

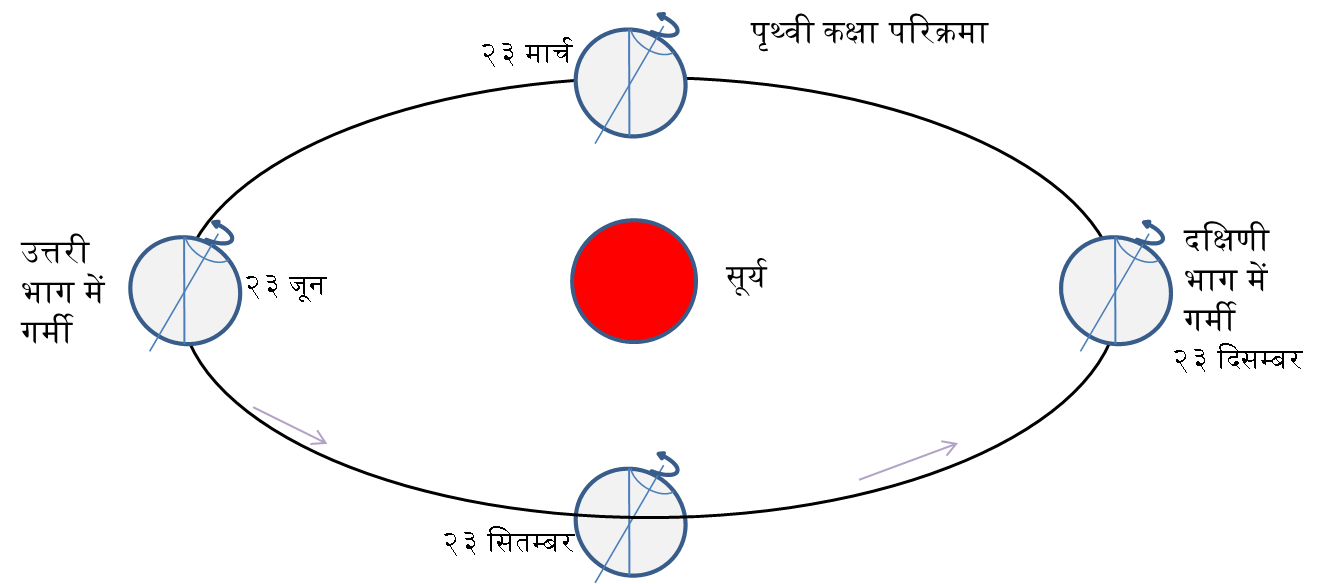
पृथ्वी की वार्षिक गति
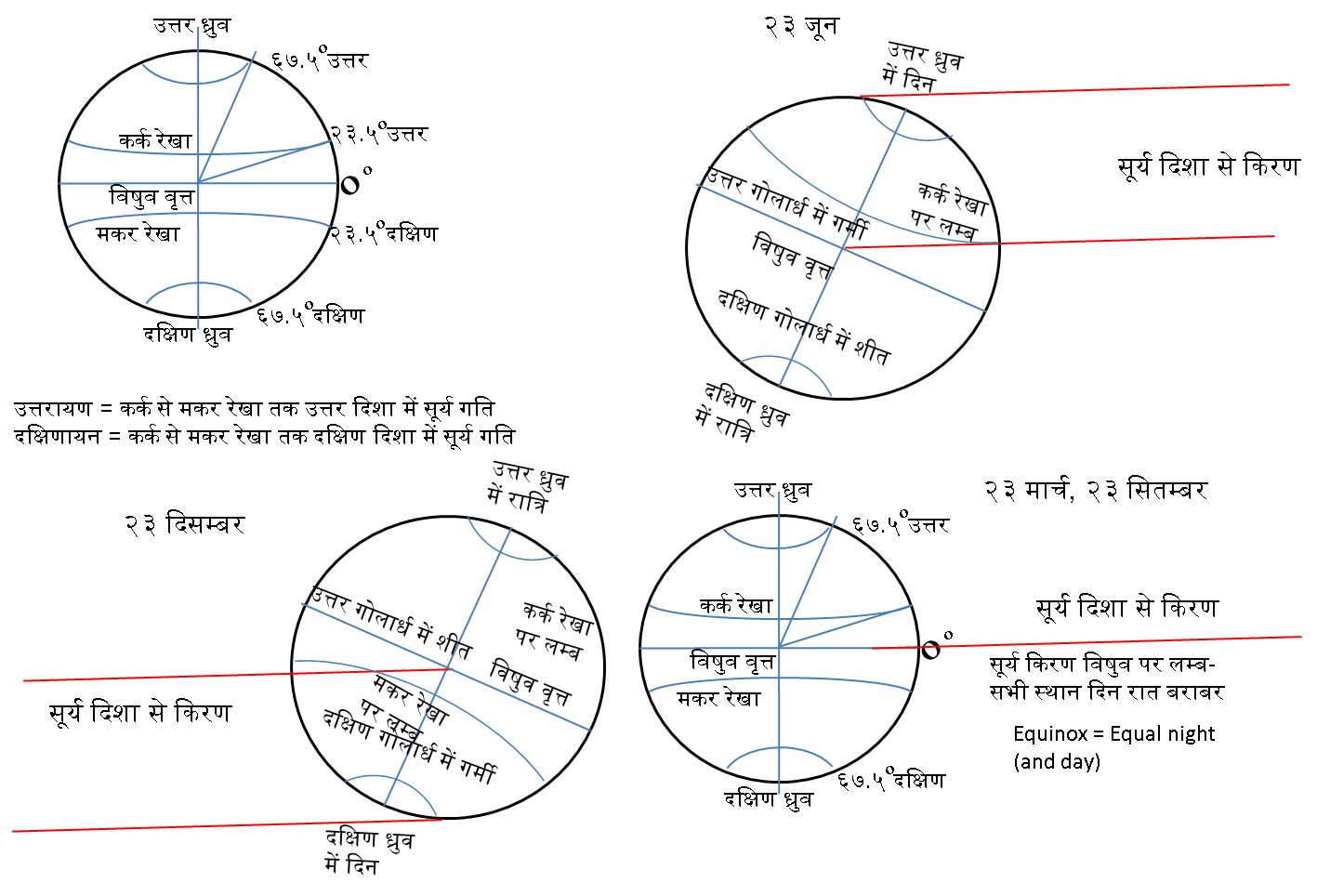
अक्ष भ्रमण और दिन
- सूर्य की १ वर्ष में ३६० अंश गति = ३६० (३६५.५) दिन
- १ दिन में गति = १ अंश
- पृथ्वी का अक्षभ्रमण २४ घण्टा = ३६० अंश
- १ अंश गति = २४ x ६०/३६० = ४ मिनट
- सूर्योदय से सूर्योदय = २४ घण्टा
- अक्ष भ्रमण = २३ घण्टा ५६ मिनट ( ४ मिनट कम)
चान्द्र परिक्रमा-मास
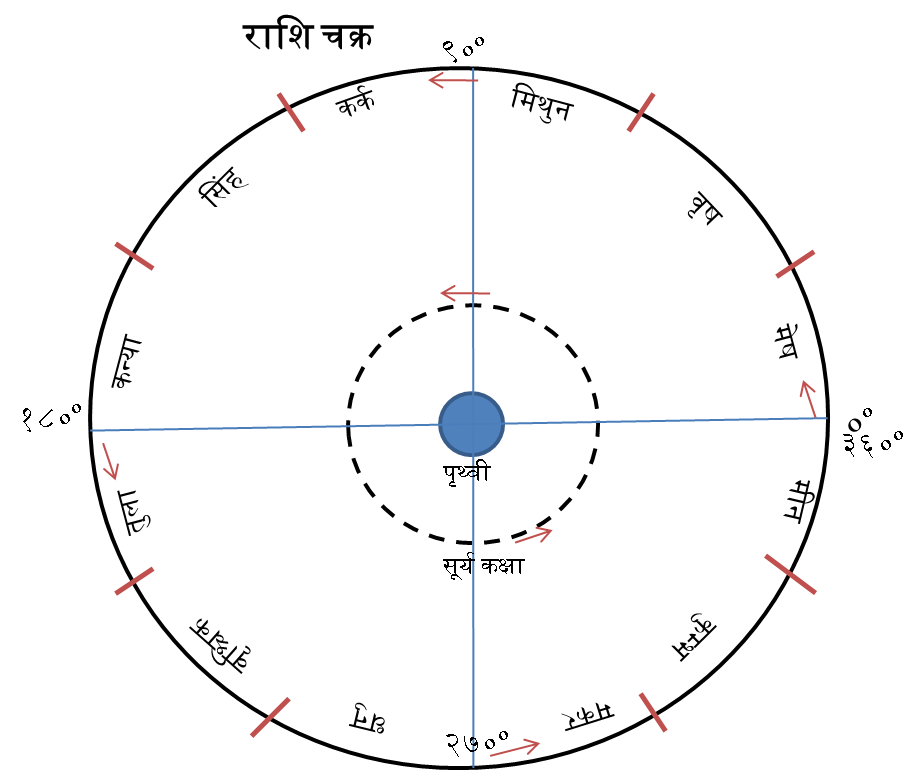
राशि-नक्षत्र
पृथ्वी से देखने पर सूर्य परिक्रमा करता हुआ दिखाई देता है।
प्रायः ३६५ दिन में परिक्रमा अतः वृत्त में ३६० अंश।
१२ चान्द्र मास (३५४ दिन) अतः वृत्त में १२ राशि
१ राशि = ३० अंश
चन्द्र परिक्रमा २७.३ दिन
अतः १ दिन की दूरी = १ नक्षत्र = ३६०/२७ =१३ २०’
१ राशि = २+१/४ नक्षत्र
नक्षत्र और तिथि
२७ नक्षत्र
१. अश्विनी
२. भरणी
३. कृत्तिका
४. रोहिणी
५. मृगशिरा
६. आर्द्रा
७. पुनर्वसु
८. पुष्य
९. अश्लेषा
१०. मघा
११. पूर्वा फाल्गुनी
१२. उत्तरा फाल्गुनी
१३. हस्त
१४. चित्रा
१५. स्वाती
१६. विशाखा
१७. अनुराधा
१८. ज्येष्ठा
१९. मूल
२०. पूर्वाषाढ़
२१. उत्तराषाढ़
२२. श्रवण
२३. धनिष्ठा
२४. शतभिषक्
२५. पूर्व भाद्रपद
२६. उत्तर भाद्रपद
२७. रेवती
मास-नाम
प्रति मास पूर्णिमा को चन्द्र जिस नक्षत्र में रहता है, मास का वही नाम होता है। जब सूर्य प्रथम राशि (मेष) या प्रथम नक्षत्र (अश्विनी) में होता है, तो चन्द्र पूर्णिमा के दिन उसके उलटा चित्रा नक्षत्र में रहेगा। अतः प्रथम मास = चैत्र। अगली पूर्णिमा को २+१/४ नक्षत्र आगे, विशाखा नक्षत्र में। द्वितीय मास = वैशाख।
१२ मास:-
१. चैत्र, २. वैशाख, ३. ज्येष्ठ, ४. आषाढ़, ५. श्रावण, ६. भाद्रपद, ७. आश्विन, ८. कार्त्तिक, ९. मार्गशीर्ष (अग्रहायण), १०. पौष, ११. माघ, १२. फाल्गुन।
अयन
मार्गशीर्ष मास में सूर्य मकर रेखा से उत्तर गति आरम्भ करता है:— ६ मास तक उत्तर गति — उत्तरायण।
आषाढ़ से दक्षिणायन ६ मास।
दोनों अयन मिला कर वर्ष = हायन।
अग्रहायन के आरम्भ का मास (मृगशिरा) = अग्रहायण।
चान्द्र तिथि
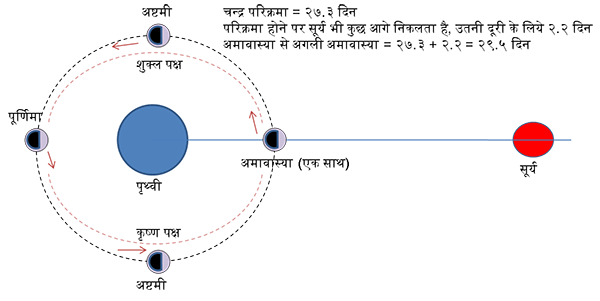
अमावास्या में सूर्य चन्द्र एक दिशा में (अमा = एक साथ, वास्य = वास)।
(चन्द्र-सूर्य) अन्तर = ० अंश।
पूर्णिमा को चन्द्र सूर्य के विपरीत = १८० अंश आगे।
अमावास्या में चन्द्र का अन्धकार भाग दीखता है। प्रकाशित भाग सूर्य की तरफ।
पूर्णिमा में पूर्ण प्रकाशित भाग दीखता है। अमावास्या से पूर्णिमा तक प्रकाशित भाग बढ़ता है— शुक्ल पक्ष।
पूर्णिमा से अमावास्या तक अन्धकार भाग बढ़ता है— कृष्ण पक्ष।
पक्ष = पार्श्व, चिड़िया का पंख। पक्ष होने से पक्षी।
१ पक्ष = १४+३/४ = प्रायः १५ दिन = १५ तिथि।
१५ तिथि में चन्द्र-सूर्य अन्तर ० से १८० अंश बढ़ता है।
अतः तिथि संख्या = (चन्द्र – सूर्य)/ १५
१८०/१५ = १२ अंश पर तिथि बदलती है।
तिथियों के नाम:—
१. प्रतिपदा
उसके बाद गिनती से:— २. द्वितीया, ३. तृतीया, ४. चतुर्थी, ५. पञ्चमी, ६. षष्ठी, ७. सप्तमी, ८ अष्टमी, ९. नवमी, १०. दशमी, ११. एकादशी, १२. द्वादशी, १३. त्रयोदशी, १४. चतुर्दशी
शुक्ल पक्ष की अन्तिम तिथि = १५. पूर्णिमा।
उसके बाद १६, १७,… ३० तक तिथि होनी चाहिये। लेकिन कृष्ण पक्ष में भी १ से गिनते हैं— प्रतिपदा, द्वितीया आदि-शुक्ल पक्ष जैसा।
अन्तिम तिथि को ३० = अमावास्या लिखते हैं।
शुक्ल प्रतिपदा— (चन्द्र- सूर्य) = १ से १२ अंश तक।
द्वितीया = १२ से २४ अंश तक।
पूर्णिमा— १६८ से १८० अंश तक।
कृष्ण पक्ष की प्रतिपदा— १८० से १९२ अंश तक
अमावास्या = ३३०-३६० अंश तक।
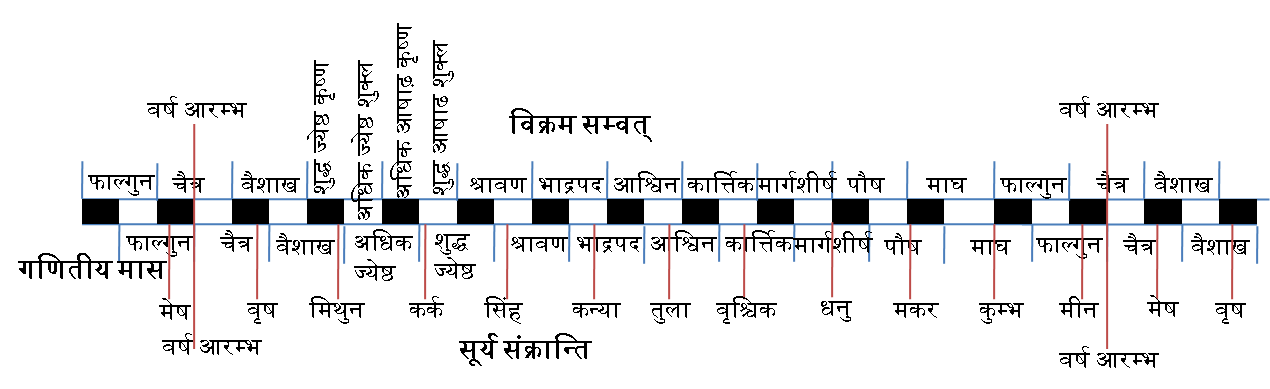
चान्द्र और सौर वर्ष
चान्द्र मास गणित अनुसार शुक्ल पक्ष से शुरु होता है। तिथि १, २, ३, ४, ५, ६, ७, ८, ९, १०, ११, १२, १३, १४, १५
उसके बाद कृष्ण पक्ष की १५ तिथि— १, २, ३, ४, ५, ६, ७, ८, ९, १०, ११, १२, १३, १४, ३०
सौर वर्ष में १२ मास— १. मेष (० से ३० अंश तक), २. वृष, ३. मिथुन, ४. कर्क, ५. सिंह, ६. कन्या, ७. तुला, ८. वृश्चिक, ९. धनु, १०. मकर, ११. कुम्भ, १२. मीन
सूर्य गति समान नहीं होने से सौर मास में २९ से ३१ दिन होते हैं। जिस चान्द्र मास में सूर्य मेष राशि में प्रवेश करता है (० अंश, मेष-संक्रान्ति), वह चैत्र मास है। इस मास की पूर्णिमा को चन्द्र चित्रा नक्षत्र में रहेगा। इसी क्रम में,
२. वृष संक्रान्ति – वैशाख मास
३. मिथुन संक्रान्ति – ज्येष्ठ मास
४. कर्क संक्रान्ति – आषाढ़ मास
५. सिंह संक्रान्ति – श्रावण मास
६. कन्या – भाद्रपद मास
७. तुला – आश्विन मास (कुमार या क्वार मास)
८. वृश्चिक – कार्त्तिक मास
९. धनु – मार्गशीर्ष मास (अग्रहायण)
१०. मकर – पौष मास
११. कुम्भ – माघ मास
१२. मीन – फाल्गुन मास (फल्गु = खाली बाल्टी, दोल पूर्णिमा)
औसत सौर मास = ३०.५ दिन, औसत चान्द्र मास = २९.५ दिन। ३० या ३१ चान्द्र मास के बाद किसी चान्द्र मास में सूर्य संक्रान्ति नहीं होती है। उसके ठीक पहले और पीछे १-१ संक्रान्ति। बाद की संक्रान्ति के अनुसार मास का नाम। उसी नाम का अधिक मास जिसमें संक्रान्ति नहीं होती।
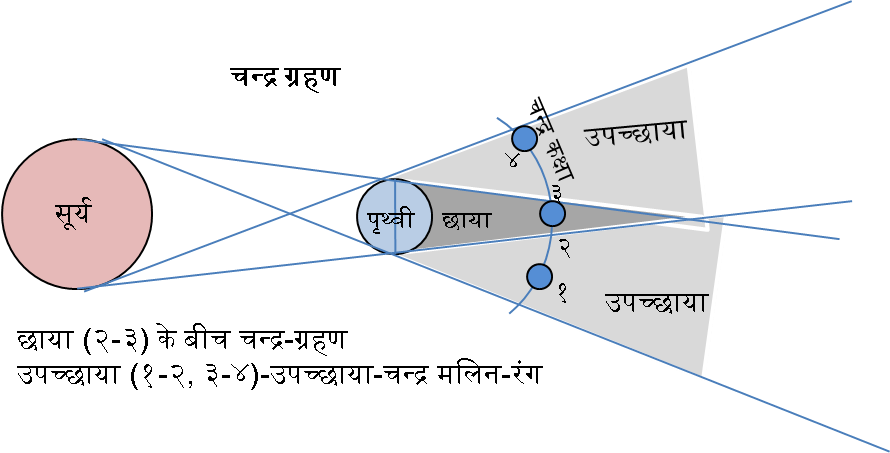
चन्द्र और सूर्य की इस परस्पर गति नीचे दर्शाये गए चित्र में देखिये।

दिन
१. सौर दिन: किसी स्थान के सूर्योदय से आगामी सूर्योदय तक। यह सामाजिक व्यवहार का दिन है।
२. छाया व्यवहार (अक्षांश, समय के लिये) के लिये मध्याह्न से दिन आरम्भ। पितर कार्य के लिये भी।
३. वेध: आकाश में ग्रह स्थिति देखने के लिये सूर्यास्त से दिन। प्रदोष, शिवरात्रि के लिये दिन का आरम्भ।
४. गणना के लिये मध्य रात्रि से दिन। किसी देशान्तर रेखा पर सभी स्थानों पर एक ही समय मध्यरात्रि (या मध्याह्न भी) होगा।
वार
इनका क्रम है:— सूर्य, चन्द्र, मंगल, बुध, गुरु, शुक्र, शनि।
यह भी सूर्योदय से होते हैं। गति बढ़ने के क्रम में ७ ग्रह हैं— शनि (सबसे धीमा होने के कारण शनैश्चर), गुरु, मंगल, सूर्य, शुक्र, बुध, चन्द्र। पृथ्वी के अक्ष भ्रमण के कारण २४ घण्टे (४ मिनट कम) में पूर्व क्षितिज पर १२ राशियों का क्रम से उदय होता है। आउसत २ घण्टॆ में एक राशि का उदय। हर राशि का दिन के दो भाग अहः + रात्र = अहोरात्र जैसे दो भाग होंगे। अहोरात्र के बीच के अक्षरों के अनुसार इसे होरा कहते हैं। हर दिन २४ होरा का उदय होता है। होरा = Hour। चन्द्र के दिन सोमवार को सूर्योदय के बाद पहली होरा चन्द्र की होगी। उसके बाद ७-७ ग्रहों के ३ चक्र होने पर २१ होरा पूर्ण होगी। फिर २२वीं होरा चन्द्र की, २३ वीं- शनि, २४वीं- गुरु की होगी। २४ होरा में दिन पूरा हो जायेगा। अगले दिन की पहली होरा (चन्द्र से २५वीं) मंगल की होगी। अतः सोमवार के बाद मंगल वार होगा। अगले दिन पहली होरा मंगल से गिनने पर ४थी बुध की होगी। इसी प्रकार क्रम से दिनों की होरा शुक्र, शनि, सूर्य से आरम्भ होगी। सूर्य-चन्द्र-मंगल-बुध-गुरु-शुक्र-शनि यह क्रम सृष्टि के आरम्भ से चला आ रहा है। दिनों की गणना की जांच करने के लिये देखते हैं कि वार ठीक आ रहा है कि नहीं। दैनिक कार्यक्रम बनाने के लिये वार का महत्त्व है। हर वार के कुछ उपयोगी या वर्जित काम हैं। इसका इतिहास में कोई महत्त्व नहीं है अतः इसका उल्लेख नहीं होता है।
तिथि
चन्द्र जब सूर्य से १२ अंश आगे निकलता है तो एक तिथि होती है।
तिथि संख्या = (चन्द्र – सूर्य) / १२ अंश
० से १ तक अर्थात् १ अंश से १२ अंश तक पहली तिथि प्रतिपदा। सूर्य से ११ अंश के भीतर चन्द्र रहने पर वह नहीं दीखता है। शुक्ल पक्ष की द्वितीया(१२ -२४ अंश) से चन्द्र दीखता है। गणना में तिथि संख्या १५ से अधिक आने पर कृष्ण पक्ष शुरु होता है और तिथि से शुक्ल पक्ष की १५ तिथि घटाते हैं।
उदाहरण- (चन्द्र – सूर्य) = २०७ अंश
१२ से भाग देने पर -१७.२५ अर्थात् १८वीं तिथि। १५ घटाने पर यह कृष्ण तृतीया हुआ। गणित के अनुसार पूरे विश्व में तिथि का आरम्भ एक ही साथ होता है। व्यवहार के लिये किसी स्थान पर सूर्योदय के समय जो तिथि होती है, वही तिथि अगले सूर्योदय तक मानी जाती है।
उदाहरण, भारतीय समय से यदि ५३० से अगले दिन ५३० तक ११ तिथि है। जिस स्थान पर ६ बजे सूर्योदय होगा वहां सूर्योदय समय ११ तिथि चल रही है, अतः वहां ११ तिथि होगी। जिस स्थान पर सूर्योदय ५ बजे है वहां १० तिथि चल रही है। अतः अगले सूर्योदय तक १० तिथि ही कही जायेगी यद्यपि सूर्योदय के ३० मिनट बाद ११ तिथि शुरु हो गयी थी।
१ दिन में २४ घण्टा = ६० दण्ड होते हैं। १ तिथि ५० से ६९ दण्ड तक होती है। अतः कभी कभी किसी तिथि में किसी स्थान पर कोई सूर्योदय नहीं होता। जैसे किसी स्थान पर ६ बजे सूर्योदय हो रहा है और ११ तिथि ६१५ से आगामी दिन ५३० तक है, तो वह दिन १० तिथि तथा अगले दिन १२ तिथि होगी। १० तिथि नहीं होगी अर्थात् क्षय तिथि होगी। तिथि में वृद्धि भी होती है अर्थात् १ तिथि में दो बार सूर्योदय होता है। पहले दिन तिथि परिवर्तन नहीं होता है, उस दिन तिथि वृद्धि (अशुद्ध तिथि) तथा अगले दिन शुद्ध तिथि होगी।

नक्षत्र
प्राचीन काल में नक्षत्र से भी तिथि कही जाती थी। चन्द्र सूर्योदय के समय जिस नक्षत्र में रहेगा वह उस दिन का नक्षत्र कहा जायेगा। राशि के साथ समन्वय के लिये नक्षत्रों के ४-४ भाग (पाद) किये गये हैं। २७ x ४ = १०८ नक्षत्र पाद होने से हर राशि में ९-९ पाद होंगे। हर पाद को १ अक्षर से सूचित करते हैं। जन्म के समय जिस नक्षत्र पाद में चन्द्र रहता है, उस अक्षर से राशिनाम होता है।
चन्द्र २७.२ दिन में पृथ्वी की परिक्रमा करता है। अतः २८ नक्षत्र की भी एक पद्धति थी। २८वां नक्षत्र अभिजित् (श्रवण के पहले) का मान चन्द्र की ०.२ दिन की गति के बराबर है। ब्रह्मा के काल में यह ध्रुव-तारा था, अर्थात् पृथ्वी के उत्तरी ध्रुव की दिशा में। प्रायः १५,८०० ईसा पूर्व में उत्तरी ध्रुव की दिशा अभिजित् से बहुत दूर हो गयी। तब कार्त्तिकेय ने धनिष्ठा से वर्ष का आरम्भ किया। किन्तु अभिजित् स्वतन्त्र नक्षत्र के रूप में माना गया जिसके स्वामी ब्रह्मा हैं। फल, मुहूर्त्त आदि के लिये अभिजित् सहित २८ नक्षत्र माने जाते हैं। चन्द्र की मध्य गति (७९०/३५/५२ कला) को सूक्ष्म नक्षत्र भोग कहते हैं। इसका डेढ़ गुणा मान इन ६ नक्षत्रों का है- रोहिणी, अनुराधा, पुनर्वसु और ३ उत्तरा (उत्तरा फाल्गुनी, उत्तराषाढ़, उत्तर-भाद्रपद, अर्थात् ४, १६, ७, १२, २१, २६ नक्षत्र)। भरणी (२), आर्द्रा (६), अश्लेषा (९), स्वाती (१५), ज्येष्ठा (१८), शतभिषक् (२४)-इन ६ नक्षत्रों का मान आधा है। शेष १५ नक्षत्र चन्द्र की मध्यम गति के बराबर हैं।
इन २७ नक्षत्रों का कुल भोग (२१३४५/४१/२५) वृत्त की कलाओं (२१६००) से घटाने पर शेष (२५४/१८/३५) २८ वें अभिजित् नक्षत्र का भोग आता है जो उत्तराषाढ़ (२१) तथा श्रवण (२२) नक्षत्रों के बीच आता है।
करण
करण = तिथि का आधा भाग करण कहलाता है। जैसे एक दिन को दो भागों में बांटकर हम दिन-रात्रि कहते हैं।
करण = (चन्द्र – सूर्य)/ ६ अंश
चान्द्र मास में ३० तिथि के ६० करण होंगे।
७ चल करण हैं, जो ७ वारों की तरह क्रम से आते रहते हैं:— बव (सिंह), बालव (बालक), कौलव (भालू), तैतिल, गर, वणिज, विष्टि (भद्रा)।
शुक्ल प्रतिपदा के द्वितीय भाग से चल करण शुरु होते हैं। ८ बार इनके चक्र के बाद ५६ करण होते हैं।
४ करण बचते हैं जो स्थिर करण हैं— कृष्ण १४, दूसरा भाग— शकुनि, अमावास्या— चतुष्पद, नाग। शुक्ल प्रतिपदा पूर्व भाग— किंस्तुघ्न।
योग
योग:— सूर्य चन्द्र का योग १ परिक्रमा (३६० अंश) में २७ योग बनाते हैं।
| १. विष्कम्भ | १०. गण्ड | १९. परिघ |
| २. प्रीति | ११. वृद्धि | २०. शिव |
| ३. आयुष्मान् | १२. ध्रुव | २१. सिद्ध |
| ४. सौभाग्य | १३. व्याघात | २२. साध्य |
| ५ शोभन | १४. हर्षण | २३. शुभ |
| ६. अतिगण्ड | १५. वज्र | २४. शुक्ल |
| ७. सुकर्मा | १६. सिद्धि | २५. ब्रह्म |
| ८. धृति | १७, व्यतीपात | २६. ऐन्द्र |
| ९. शूल | १८. वरीयान् | २७. वैधृति |

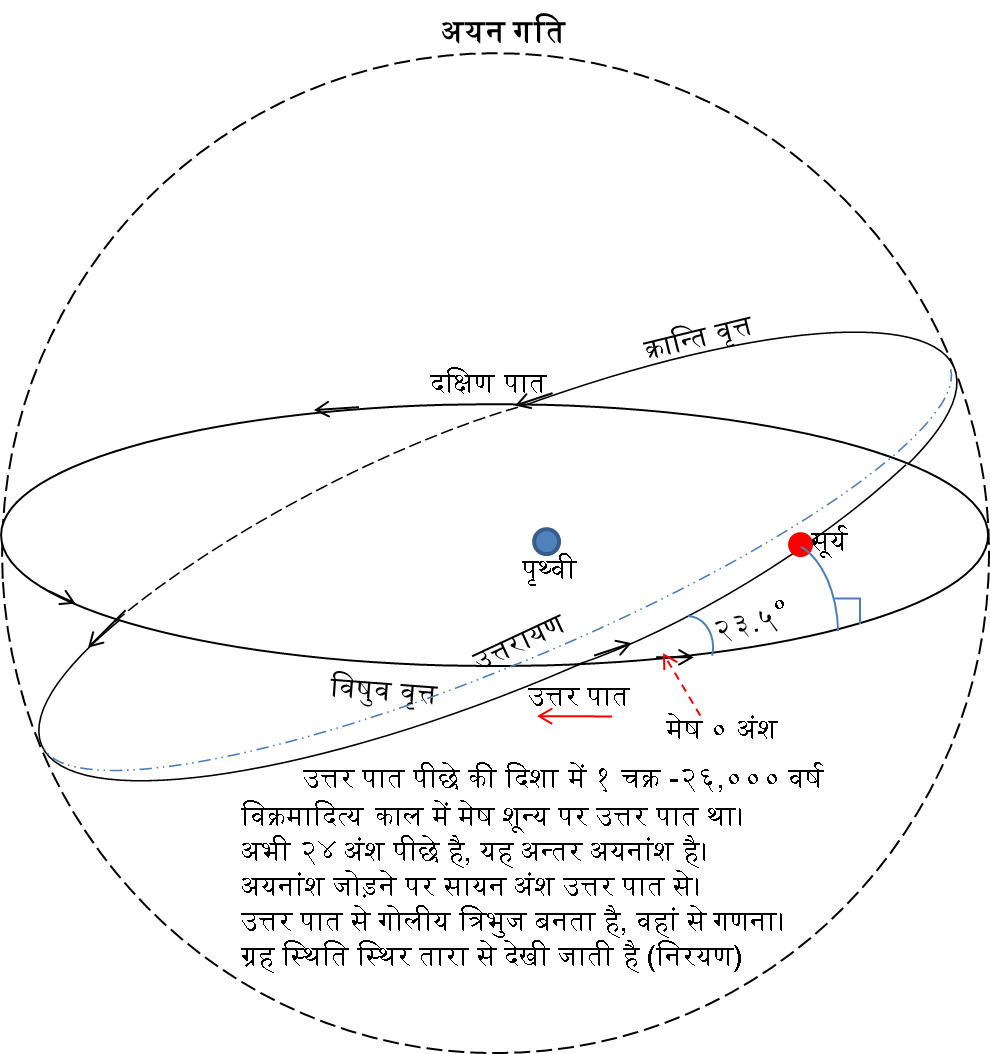


अयन चक्र तथा युग
ज्योतिष का युग ४३,२००० वर्ष का है। जिसमें शनि तक के ग्रह पूरा चक्र लगाते हैं। ऐतिहासिक युग २४,००० वर्ष का है जो जल प्रलय का चक्र है। पृथ्वी के उत्तरी भाग में अधिक स्थल भाग है। इसमें अधिक गर्मी २ कारण से है:—
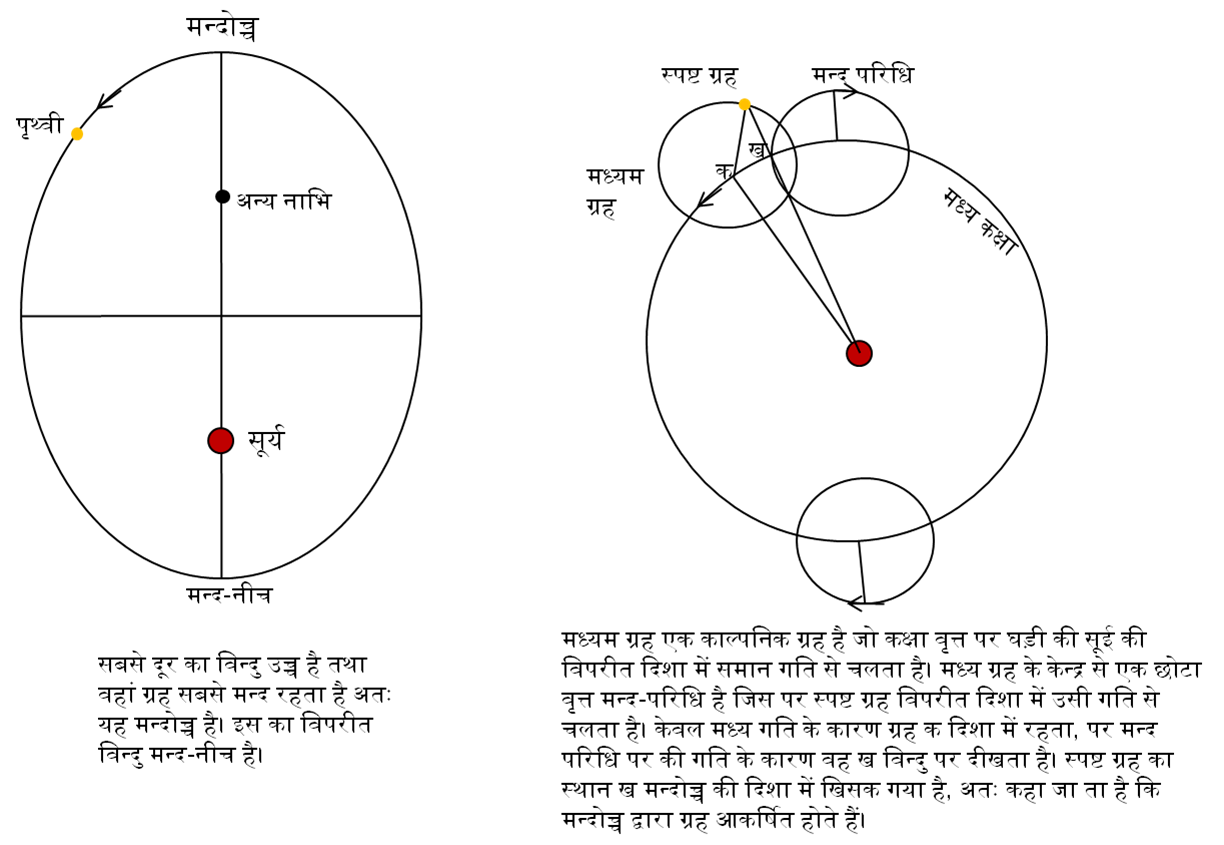
०१. पृथ्वी सूर्य के निकट हो — मन्द नीच पर
०२. उत्तरी ध्रुव सूर्य की तरफ झुका हो — उत्तरायण का अन्त।
दोनों जब एक साथ हों तो जल प्रलय होगा। दोनों उलटी दिशा में हों तो हिम युग होगा, ध्रुव प्रदेश की बर्फ दक्षिण तक फैल जायेगी। मन्दोच्च (या नीच) तथा अक्ष दिशा का चक्र विपरीत दिशा में हैं— १ लाख तथा २६,००० वर्ष में। दोनों मिला कर २१,६०० वर्ष का हिम चक्र आधुनिक सिद्धान्त के अनुसार है— १/१००,००० + १/२६,००० = १/२१,६००
किन्तु भारतीय सिद्धान्त में मन्दोच्च का दीर्घकालिक चक्र ३१२,००० वर्ष का लिया है। २४००० वर्ष में प्रथम १२,००० वर्ष अवसर्पिणी, उसके बाद १२,००० वर्ष उत्सर्पिणी।
१/२६,००० + १/३१२,००० = १/२४,०००
१२,००० वर्ष में कलि, द्वापर, त्रेता, सत्य युग १,२,३,४ अनुपात में हैं— १२००, २४,००, ३६,००, ४८,०० वर्ष के। अवसर्पिणी में सत्य युग से कलि तक, उसके बाद उत्सर्पिणी में कलिसे सत्य युग तक। अवसर्पिणी त्रेता में जल प्रलय, उत्सर्पिणी त्रेता में हिम युग होता है। वास्तविक हिमयुगों के हिसाब से यह अधिक ठीक है। २४००० वर्ष काल को ब्रह्माब्द या अयनाब्द कहा है, अभी तीसरा अयनाब्द है। तीसरा अयनाब्द में अवसर्पिणी कलि ३१०२ ई.पू. से है। उससे १०,८०० वर्ष पूर्व वैवस्वत मनु से सत्य युग, त्रेता, द्वापर बीते। वैवस्वत मनु (१३९०२ ई.पू.) से २४००० वर्ष पूर्व ३७९०२ ई.पू.से द्वितीय अयनाब्द।
द्वितीय अयनाब्द के त्रेता में २९१०२ ई.पू. स्वायम्भुव मनु = ब्रह्मा थे। उनके परिवार में ध्रुव काल में ध्रुव तारा की दिशा में उत्तरी ध्रुव था (२७,३७६ ई.पू.), कश्यप (१७५०० ई.पू.), पृथु (१७१०० ई.पू.), कार्त्तिकेय १५८०० ई.पू. में थे। वैवस्वत मनु के बाद वैवस्वत यम कल में जल प्रलय (१०,०००-९५०० ई.पू.) हुआ। उसके बाद ऋषभ देव ९५०० ई.पू.। इक्ष्वाकु (८५७६ ई.पू.) से सूर्यवंश। परशुराम के देहान्त के बाद ६१७७ ई.पू से कलम्ब सम्वत् (केरल का कोल्लम)। कलि (३१०२ ई.पू.) के ३०४४ वर्ष बाद विक्रमादित्य का विक्रम सम्वत्। कलियुग आरम्भ में शुक्ल पक्ष से मास आरम्भ। २६००० वर्ष के अयन चक्र के कारण २१०० वर्ष में ऋतु १ मास पीछे । विक्रम सम्वत् आरम्भ में १.५ मास पीछे खिसकने के कारण मास आरम्भ कृष्ण पक्ष से।
भारत के मुख्य कैलेण्डर
०१. स्वायम्भुव मनु (२९१०२ ई.पू.) से— ऋतु वर्ष के अनुसार-विषुव वृत्त के उत्तर और दक्षिण ३-३ पथ १२, २०, २४ अंश पर थे जिनको सूर्य १-१ मास में पार करता था। उत्तर दिशा में ६ तथा दक्षिण दिशा में भी ६ मास। (ब्रह्माण्ड पुराण १/२२ आदि)। इसे पुरानी इथिओपियन बाइबिल में इनोक की पुस्तक के अध्याय ८२ में भी लिखा गया है।
०२. ध्रुव— इनके मरने के समय २७३७६ ई.पू. में ध्रुव सम्वत्, जब उत्तरी ध्रुव पोलरिस (ध्रुव तारा) की दिशा में था।
०३. क्रौञ्च सम्वत्— ८१०० वर्ष बाद १९२७६ ई.पू. में क्रौञ्च द्वीप (उत्तर अमेरिका) का प्रभुत्व था (वायु पुराण, ९९/४१९)।
०४. कश्यप (१७५०० ई.पू.) भारत में आदित्य वर्ष— अदितिर्जातम् अदितिर्जनित्वम्-अदिति के नक्षत्र पुनर्वसु से पुराना वर्ष समाप्त, नया आरम्भ। आज भी इस समय पुरी में रथ यात्रा होती है।
०५. कार्त्तिकेय— १५८०० ई.पू.-उत्तरी ध्रुव अभिजित् से दूर हट गया। धनिष्ठा नक्षत्र से वर्षा तथा सम्वत् का आरम्भ। अतः सम्वत् को वर्ष कहा गया। (महाभारत, वन पर्व २३०/८-१०)
०६. वैवस्वत मनु— १३९०२ ई.पू.-चैत्र मास से वर्ष आरम्भ। वर्तमान युग व्यवस्था।
०७. वैवस्वत यम— ११,१७६ ई.पू. (क्रौञ्च के ८१०० वर्ष बाद)। इनके बाद जल प्रलय। अवेस्ता के जमशेद।
०८. इक्ष्वाकु— १-११-८५७६ ई.पू. से। इनके पुत्र विकुक्षि को इराक में उकुसी कहा गया जिसके लेख ८४०० ई.पू. अनुमानित हैं।
०९. परशुराम— ६१७७ ई.पू. से कलम्ब (कोल्लम) सम्वत्।
१०. युधिष्ठिर काल के ४ पञ्चाङ्ग—
(क) अभिषेक- १७-१२-३१३९ ई.पू. (इसके ५ दिन बाद उत्तरायण में भीष्म का देहान्त)
(ख) ३६ वर्ष बाद भगवान् कृष्ण के देहान्त से कलियुग १७-२-३१०२ उज्जैन मध्यरात्रि से। २ दिन २-२७-३० घंटे बाद चैत्र शुक्ल प्रतिपदा।
(ग) जयाभ्युदय- ६मास ११ दिन बाद परीक्षित अभिषेक २२-८-३१०२ ई.पू. से।
(घ) लौकिक- ध्रुव के २४३०० वर्ष बाद युधिष्ठिर देहान्त से, कलि २५ वर्ष = ३०७६ ई.पू से कश्मीर में (राजतरंगिणी)।
११. भटाब्द— आर्यभट-कलि ३६० = २७४२ ई.पू से।
१२. जैन युधिष्ठिर शक— काशी राजा पार्श्वनाथ का सन्यास-२६३४ ई.पू. (मगध अनुव्रत-१२वां बार्हद्रथ राजा)।
१३. शिशुनाग शक— शिशुनाग देहान्त १९५४ ई.पू. से (बर्मा या म्याम्मार का कौजाद शक)।
१४. नन्द शक— १६३४ ई.पू. महापद्मनन्द अभिषेक से। ७९९ वर्ष बाद खारावेल अभिषेक।
१५. शूद्रक शक— ७५६ ई.पू.-मालव गण आरम्भ।
१६. चाहमान शक— ६१२ ई.पू. में (बृहत् संहिता १३/३)-असीरिया राजधानी निनेवे ध्वस्त।
१७. श्रीहर्ष शक— ४५६ ई.पू.-मालव गण का अन्त।
१८. विक्रम सम्वत्— उज्जैन के परमार राजा विक्रमादित्य द्वारा ५७ ई.पू. से।
१९. शालिवाहन शक— विक्रमादित्य के पौत्र द्वारा ७८ ई.से।
२०. कलचुरि या चेदि शक— २४६ ई.।
२१. वलभी भंग (३१९ ई.) गुजरात के वलभी में परवर्त्ती गुप्त राजाओं का अन्त।
विदेशी कैलेण्डर
०१. इनोक— इथिओपिया की पुरानी बाइबिल के भाग ३ इनोक के अध्याय ७२-८१ में। वर्ष के ४ भाग ९१-९१ दिनों के, उसके बाद १ दिन छुट्टी। ९१ दिन में विषुव के उत्तर या दक्षिण के ३-३ मार्ग पर १-१मास सूर्य। बाइबिल (जेनेसिस ५/२१-इनोक की आयु ३६५ वर्ष)।
०२. मिस्र— ३०-३० दिनों के १२ मास। अन्त में ५ दिन जोड़ते थे। भारत में १२ x ३० दिनों का वत्सर, उसके बाद पाञ्चरात्र, कभी कभी षडाह। सिरियस तारा (मिस्र में थोथ) के उदय से थोथ मास और वर्ष आरम्भ। १४६० वर्ष के बाद १ वर्ष जोड़ते थे।
०३. सुमेरिया— चान्द्र सौर वर्ष में ३५४, ३५५, ३८३, ३८४ दिन। दो प्रकार से अधिक मास की गणना।
(क) अष्टक— ८ ऋतु वर्ष = २९२१.९४ दिन, ९९ चान्द्र मास ( ३ अधिक) = २९२३.५३ दिन।
(ख) ३८३ ई.पू. से— मेटन चक्र-१९ सौर वर्ष = ६९३९.६० दिन, २३५ चान्द्र मास (७ अधिक) = ६९३९.६९ दिन।
०४. यहूदी वर्ष— ७/८-१०-३७६१ ई.पू. (रवि-सोम वार के बीच की मध्यरात्रि से) ११ बजे ११मिनट २० सेकण्ड से। यहूदी वर्ष ३८३१ (७१ ई.) में यहूदी राज्य नष्ट।
०५. इरानी—
(क) दारा (Darius)— ५२० ई.पू. से-३६५ दिनों के १२ सौर मास। १२० वर्ष के बाद ३० दिनों का अधिक मास।
(ख) तारीख-ए-जलाली— १०७४ ई. में सेल्जुक राजा जलालुद्दीन मलिक द्वारा-३६५ दिनों के ३३ वर्षों के बाद ८ दिन अधिक।
(ग) पहलवी (तमिल का पल्लव-शक्तिशाली, पहलवान)— १९२० ई. में रजा शाह पहलवी द्वारा-पुराने नामों के साथ सौर वर्ष।
०६. असीरिया में ७४७ ई.पू. में नबोनासिर (लवणासुर)— इसके दमन के लिये भारत में ७५६ ई.पू. में शूद्रक की अध्यक्षता में मालव-गण।
०७. सेलुसिड— ३१२ ई.पू.-सुमेरियन नकल पर ग्रीक सेनापति सेल्यूकस द्वारा।
०८. जुलियन— रोमन राजा जुलियस सीजर द्वारा-उत्तर यूरोप में २ मास बर्फ से ढंके रहते थे अतः बाकी ३०४ दिनों के १० मास होते थे। नुमा पोम्पियस ने ६७३ ई.पू. में २ मास जोड़ कर ३५५ दिनों का वर्ष शुरु किया। जनवरी से वर्ष का अन्त तथा आरम्भ (जानुस देवी का दोनों तरफ मुंह-जैसे अदिति का या विक्रम सम्वत् का चैत्र मास)। फरवरी के बाद २ या ३ वर्ष पर २२ या २३ दिन का अधिक मास मरसिडोनियस जोड़ते थे। ४६ ई.पू. में जुलियस सीजर ने मिस्र से सम्पर्क होने के बाद उत्तरायण से सौर वर्ष आरम्भ करने का आदेश दिया। पर लोगों ने ७ दिन बाद जब विक्रम सम्वत् गत वर्ष १० का पौष मास आरम्भ हो रहा था, उस दिन से नया वर्ष शुरु किया (१-१-४५ ई.पू.)। मूल वर्ष आरम्भ तिथि को कृष्ण-मास (सबसे लम्बी रात) कहा गया जो आजकल क्रिस्मस है। प्रायः ४०० वर्ष बाद कौन्स्टैण्टाइन ने ईसा के काल्पनिक जन्म के अनुसार इसका आरम्भ ४५ वर्ष बाद से कर दिया। प्रतिवर्ष ३६५ दिन का होता था तथा ४ वर्ष में १ दिन अधिक था।
०९. हिजरी वर्ष— १९-३-६२२ ई. से विक्रम वर्ष ६७९ के आरम्भ के साथ हिजरी वर्ष पैगम्बर मुहम्मद द्वारा आरम्भ हुआ। अरब में पञ्चांग गणना (कलन) करने वालों को कलमा कहते थे। इसी परिवार में मुहम्मद का जन्म हुआ था। ६३२ ई. में उनके देहान्त तक ३ अधिक मास जोड़े गये। अन्तिम मास में हज के समय अधिक मास का फैसला होता था। पैगम्बर के देहान्त के बाद इसका निर्णय करने वाला कोई नहीं रहा और यह पद्धति बन्द हो गयी (अल बरूनी द्वारा-प्राचीन देशों की काल गणना)। इसकी गणना ब्रह्मगुप्त के ब्राह्म स्फुट सिद्धान्त पर आधारित थी अतः खलीफा अल-मन्सूर के समय इसका अरबी अनुवाद हुआ। ब्रह्म = अल-जबर (महान्), स्फुट सिद्धान्त = उल-मुकाबला। इसमें पहले गणित भाग था॥ अतः अल-जबर-उल-मुकाबला से बीजगणित का नाम अलजेब्रा हुआ।
१०. ग्रेगरी— १७५२ ई. में ब्रिटेन में ग्रेगरी ने जुलियन कैलेण्डर में संशोधन किया। ४ दिनों में लीप वर्ष (३६६ दिनका) जारी रहा, पर शताब्दी वर्षों में केवल उन्हीं शताब्दी वर्षों मॆं रहा जो ४०० से विभाजित हों। १ ई. से गणना में ११ दिन की अधिक गिनती होने के कारण ३ सितम्बर को १४ सितम्बर कहा गया।
अहर्गण माप
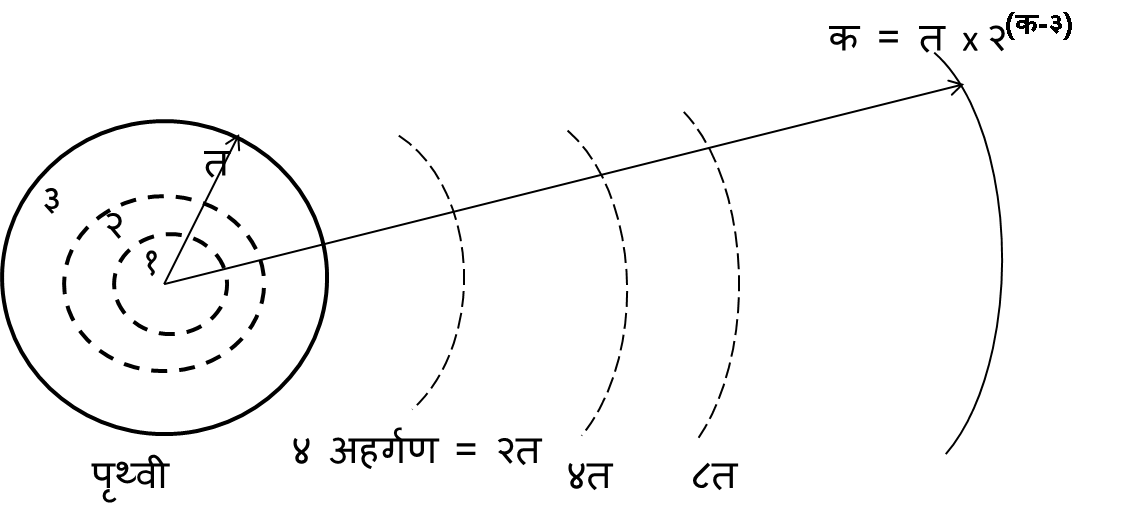
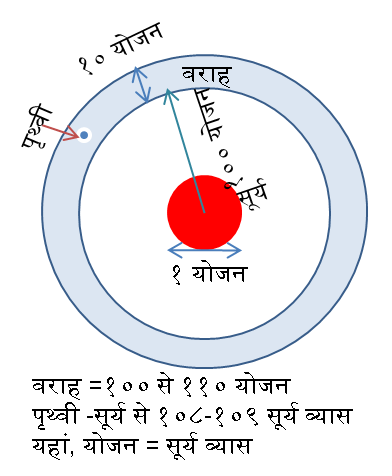
१७ अहर्गण तक पृथ्वी

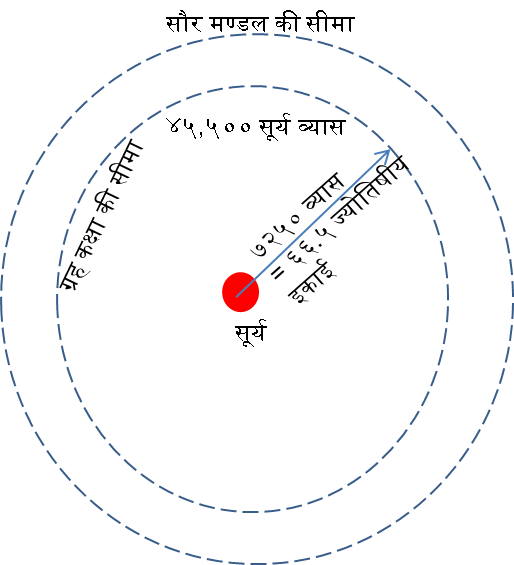
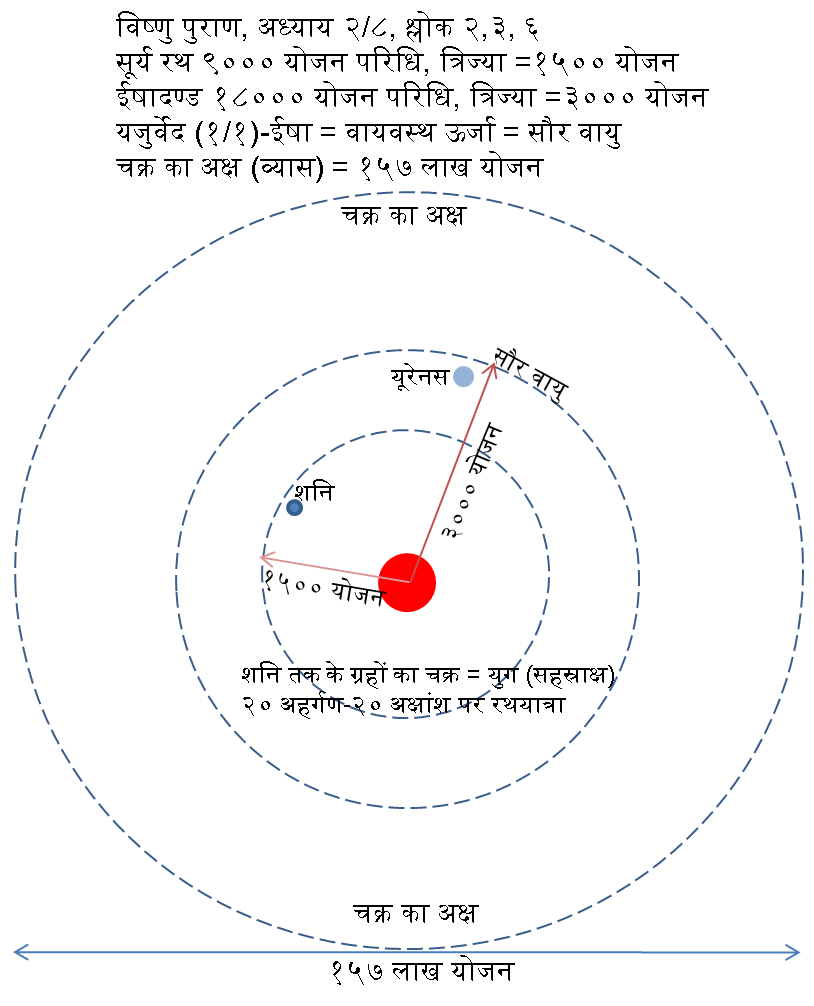
सौर मण्डल

सौर मण्डल - विष्णु के पद



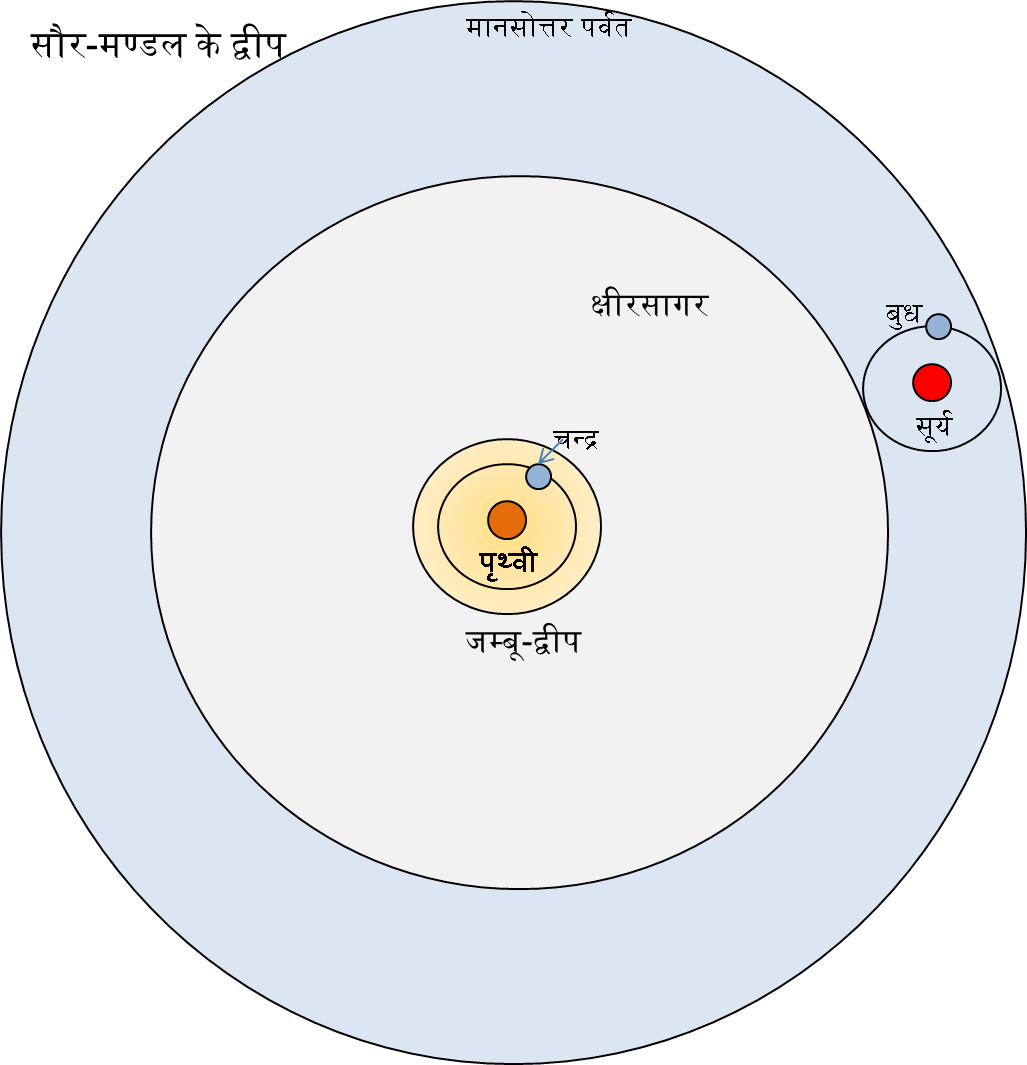
सौर-मण्डल के द्वीप
| क्रम | त्रिज्या | चौड़ाई | नाम |
|---|---|---|---|
| ०१. | ५० | ५० | जम्बूद्वीप |
| ०२. | १५० | १०० | लवणसमुद्र |
| ०३. | ३५० | २०० | प्लक्ष द्वीप |
| ०४. | ५५० | २०० | इक्षुरससागर |
| ०५. | ९५० | ४०० | शाल्मली द्वीप |
| ०६. | १,३५० | ४०० | मद्य समुद्र |
| ०७. | २,१५० | ८०० | कुश द्वीप |
| ०८. | २,९५० | ८०० | घृतसमुद्र |
| ०९. | ४,५५० | १,६०० | क्रौञ्च द्वीप |
| १०. | ६,१५० | १,६०० | क्षीरसागर |
| ११. | ९,३५० | ३,२०० | शकद्वीप |
| १२. | १२,५५० | ३,२०० | दधिसमुद्र |
| १३. | १५,७५० | ३,२०० | मानसोत्तर पर्वत |
| १४. | १८,९५० | ३,२०० | पुष्कर द्वीप |
| १५. | २५,३५० | ६,४०० | मधुरजल समुद्र |
| १६. | ४१,१०० | १५,७५० | जनस्थान |
| १७. | १,२५,००० | ८३,९०० | हिरण्य वर्ष |
| १८. | २,५०,००० | १,२५,०० | आलोक वर्ष |

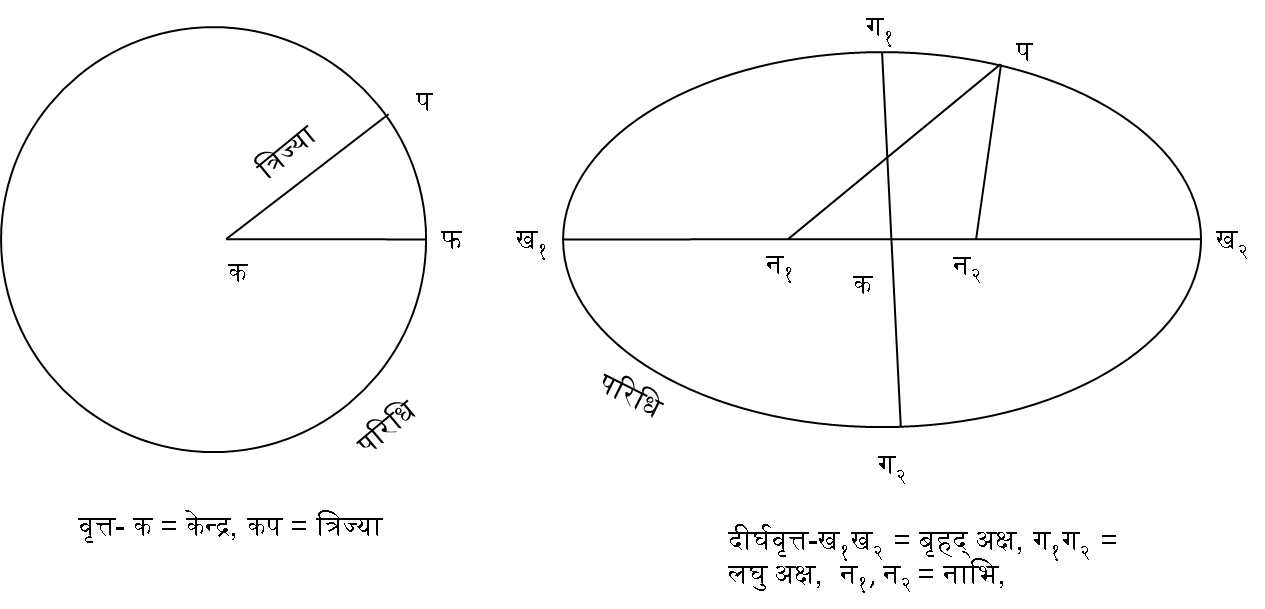
उत्क्रम वर्ग नियम


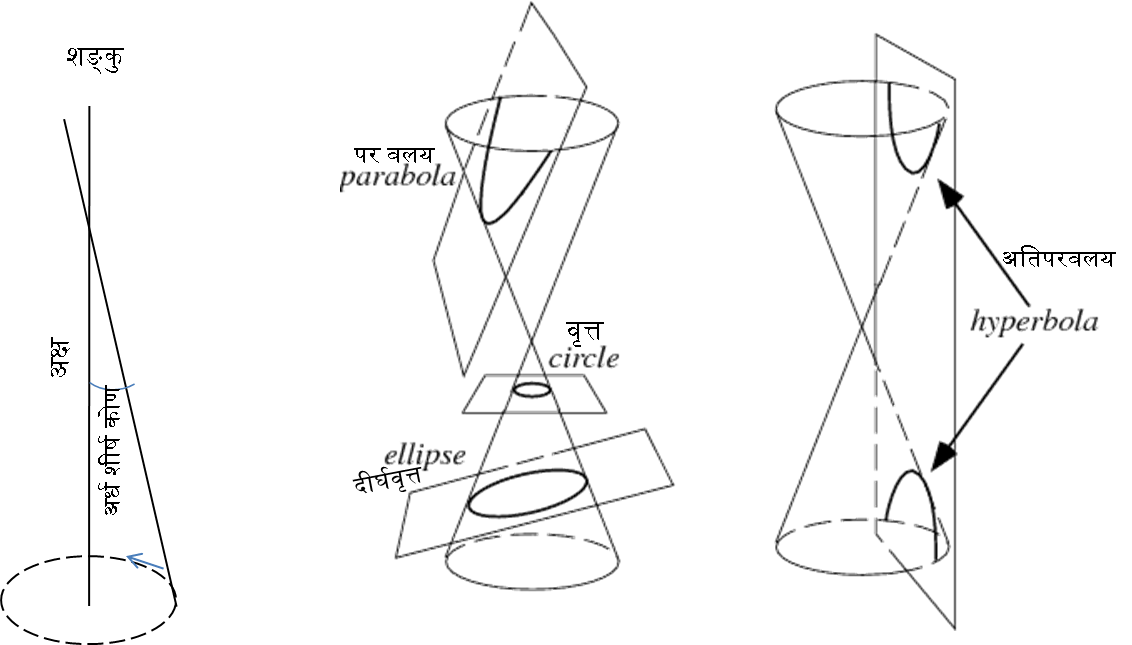
शङ्कु और उसके छेद
गुरुत्व क्षेत्र में वृत्त में गति अपसारक बल = गुरुत्व
गति थोड़ा अधिक होने पर— दीर्घवृत्त
गुरुत्व सीमा से बाहर निकलने की गति— परवलय
उससे भी अधिक गति— अतिपरवलय
वृत्त की गति से कम होने पर वह केन्द्र के निकट जायेगा।
गति बढ़ जाने से निकट कक्षा में। बहुत कम होने से केन्द्र में लीन।








????प्रणाम???? अति दिव्य और ज्ञान वर्धक लेख ।
साधुवाद ????जय श्री कृष्ण????????
आदरणीय महोदयश्री
आपके माध्यम से ज्योतिष का दर्पण अत्यधिक अधिक जानकारी के साथ प्रदान किया
अत्यधिक प्रसन्नता के साथ साधुवाद
आपका भवदीय
लाभशंकर जोशी
मोडासा गुजरात
Itne jatil wishay ko itni saral bhasha me likha hai Jo ki lagbhag asambhav tha. Aapko koti dhanyawad, sadhuwad .
Very Informative & Very Useful
Very good work
Work is highly appreciated..such more affordable work awaited.. basics of astrology can be added for new learner..
Real very nice information all real fantastic
बहुत ही उत्तम ज्योतिषीय गणना
Real very nice information
बहुत ही अच्छा और सुलभ शब्दो मे लिखकर हमारे ज्ञान मे बडावा देने का काम इस लेख ने किया इस लिये मै लेखक का शुक्रगुजार हुं।।
पंडितजी,
सादर प्रणाम !
आपने लिखे इस लेखसे साधारण व्यक्ती भी आकाशमंडल तथा पंचाग क्या होता है यह समझ सकता है।
एक बिनती और यह की, ज्योतिष/कुंडली पर एक लेख जरूर लिखे, जिसमें कुंडली के बारा घर में ग्रह और राशीयाँ कैसी आती है,उसके परिणाम क्या होते है, बारा भाव क्या है इत्यादी का परामर्श लिजीए ।
सुरेश जोशीकाका
औरंगाबाद महाराष्ट्र
Nice Sir
विशेषकर नई पीढ़ी को अवश्य पड़ना चाहिए। ज्योतिष के बिना हिंदू धर्म को समझना संभव नही और इसके लिए यह सरल-संपूर्ण और गागर में सागर है। लेखक और संपादक महोदय को साधुवाद।
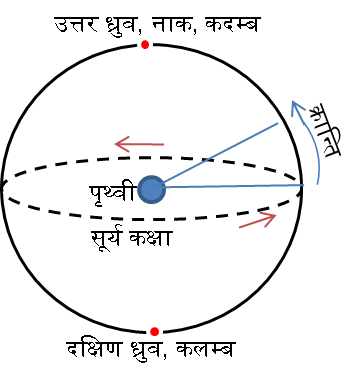
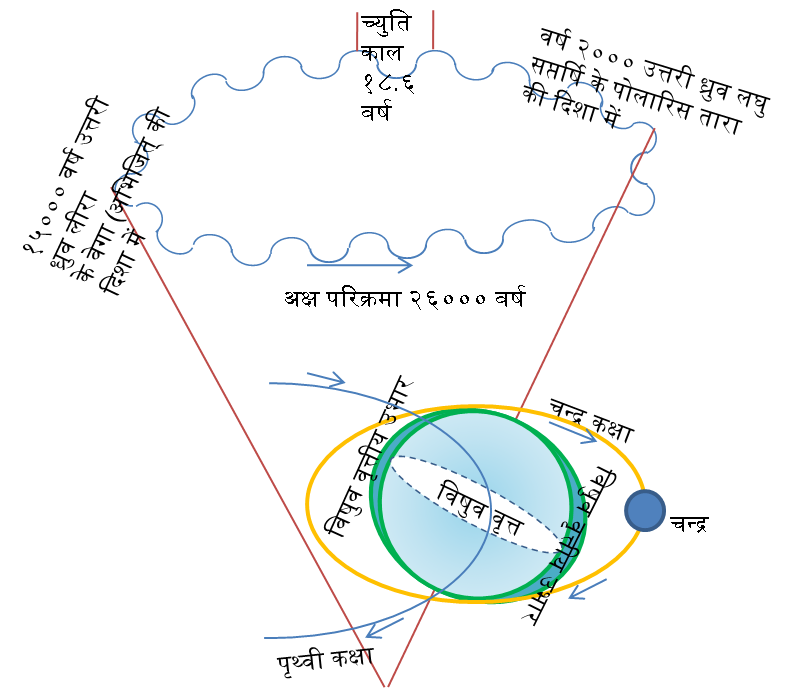
पृथ्वी अक्ष की परिक्रमा २६,००० वर्ष का है और अक्ष झुकाव २२.५ से २६ अंश तक का चक्र ४१,००० वर्ष का हैं| ऐसा संलग्न चित्र के साथ विवरण दिया गया हैं|
दूसरे चित्र मे च्युति काल १८.६ वर्ष का दिया गया हैं| यह च्युति काल क्या है? यहाँ मुझे एक भ्रम है कि, यदि च्युति काल अक्ष झुकाव २२.५ से २६ अंश के बीच का दोलन काल है तो फिर वह ४१,००० वर्ष का कैसे?
काल गणना पर इतना व्यापक और सारगर्भित लेख मै प्रथमतः पढ़ पाया हूँ| सादर धन्यवाद!
च्युति का कई प्रकार से अनुवाद किया गया है। केतकर जी इसे दीर्घवृत्तीय कक्षा का वृत्त से अन्तर (eccentricity) कहते हैं। यहां यह चन्द्र-पात (राहु) के कारण दोलन है।
मैं रामचंद्र पाण्डेय, ग्राम farna आरा, आपको सादर प्रणाम करता हूँ। मेरे ममेरे भाई चि. रामकृष्ण के यहाँ से यह पुस्तक मुझे प्राप्त हुई। ज्योतिष के साथ साथ गणित, साहित्य तथा विज्ञान और इतिहास की अदभुत जानकारी प्राप्त हुई। मैं मंत्रमुग्ध हूँ। धन्यवाद।
Short and beautiful description.
बहुत लघु रूप में शानदार विवेचन।
भारतीय ज्योतिष के गणित खण्ड पर इतने शानदार विजुअल और सरल प्रकार से फ्लो के साथ लिखा लेख मैंने बीस साल में पहली बार पढ़ा है। लेखक और संपादक दोनों को साधूवाद।
सौरमण्डलीय सिम्युलेशन ०२.
दिए गए लिंक पर आप कंट्रोल्स का प्रयोग कर के त्रिआयामी रूप में सौर-मण्डल का अनुभव कर सकते हैं। Top-Right corner पर कंट्रोल्स मिलेंगे। निश्चित ही शुद्ध अनुभव के लिए स्मार्टफोन पर्याप्त नहीं होगा या सिम्युलेशन डेस्कटॉप कंप्यूटर पर ज्यादा सही कार्य करेगा। ‘Time Control’ वाले कण्ट्रोल में स्लाइडर को माउस से नियंत्रित किया जा सकता है जो अनुपातिक रूप से सभी पिण्डों की गति को न्यूनाधिक करके दिखायेगा। स्लाइडर को माउस से घुमाने की अपेक्षा उसके बगल में दिए टेक्स्ट बॉक्स में आप टाइम को इनपुट करें तो ज्यादा सटीकता से नियन्त्रण कर पाएंगे। समय उसमें अत्यधिक कम ही डालना होगा जैसे 0.000050, अर्थात सेकंड के बहुत छोटे से हिस्से को।
माउस के व्हील से आप ज़ूम इन / ज़ूम आउट भी कर सकते हैं। माउस पॉइंटर से ड्रैग करके त्रिआयामी आकाशीय स्थिति को घूमा-फिर भी सकते हैं।
http://lvapeab.github.io/solar_system_demo.htm
सौरमण्डलीय सिम्युलेशन ०१
इस एम्बेड कोड में आप कंट्रोल्स का प्रयोग करके त्रिआयामी स्थितियों को और अधिक मजे से देख-अनुभव कर सकते हैं।